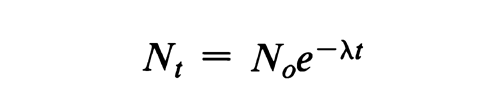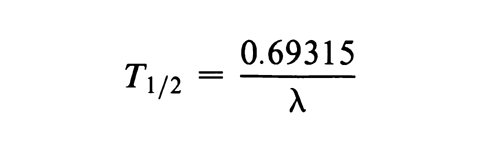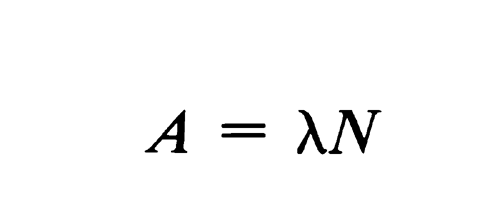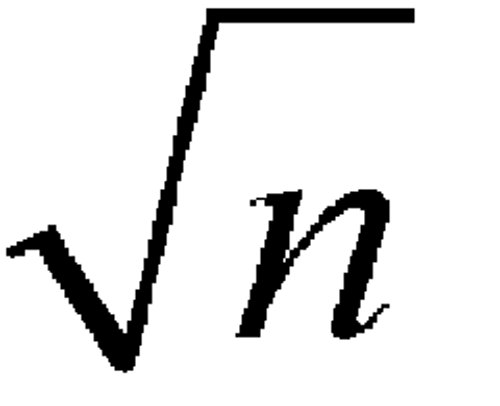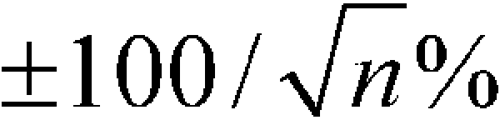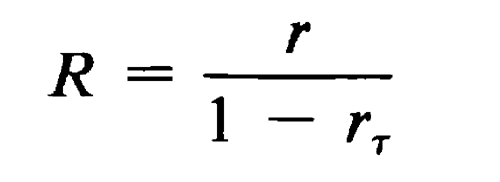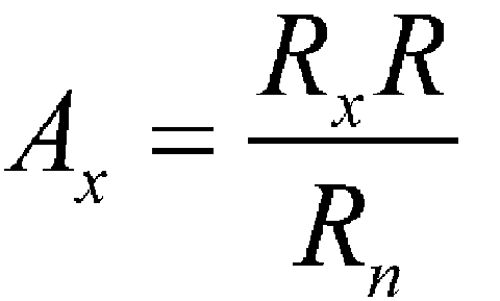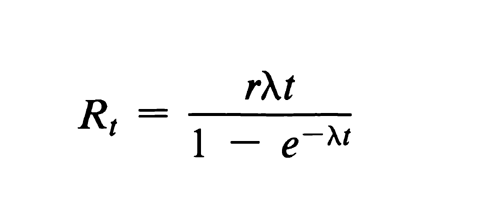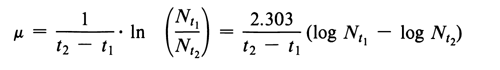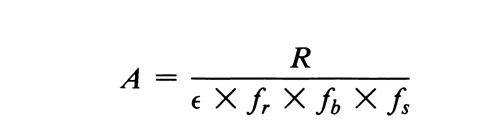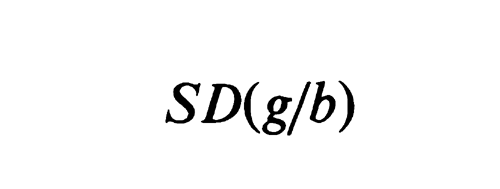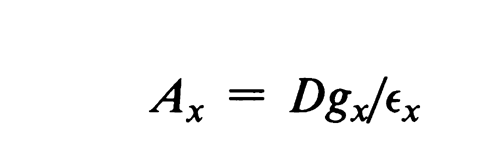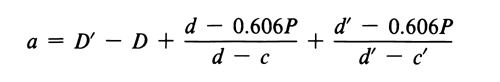Radioactive pharmaceuticals require specialized techniques in their handling and testing in order that correct results may be obtained and hazards to personnel be minimized. All operations should be carried out or supervised by personnel having had expert training in handling radioactive materials.
The facilities for the production, use, and storage of radioactive pharmaceuticals are generally subject to licensing by the federal Nuclear Regulatory Commission, although in certain cases this authority has been delegated to state agencies. The federal Department of Transportation regulates the conditions of shipment of radioactive materials. State and local agencies often have additional special regulations. Each producer or user must be thoroughly cognizant of the applicable regulations of the federal Food, Drug, and Cosmetic Act, and any additional requirements of the U. S. Public Health Service and of state and local agencies pertaining to the articles concerned.
Definitions, special considerations, and procedures with respect to the Pharmacopeial monographs on radioactive drugs are set forth in this chapter.
GENERAL CONSIDERATIONS
Fundamental Decay Law
The decay of a radioactive source is described by the equation:
in which Nt is the number of atoms of a radioactive substance at elapsed time t, No is the number of those atoms when t = 0, and 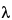 is the transformation or decay constant, which has a characteristic value for each radionuclide. The half-life, T1/2, is the time interval required for a given activity of a radionuclide to decay to one-half of its initial value, and is related to the decay constant by the equation:
is the transformation or decay constant, which has a characteristic value for each radionuclide. The half-life, T1/2, is the time interval required for a given activity of a radionuclide to decay to one-half of its initial value, and is related to the decay constant by the equation:
The activity of a radioactive source (A) is related to the number of radioactive atoms present by the equation:
from which the number of radioactive atoms at time t can be computed, and hence the mass of the radioactive material can be determined.
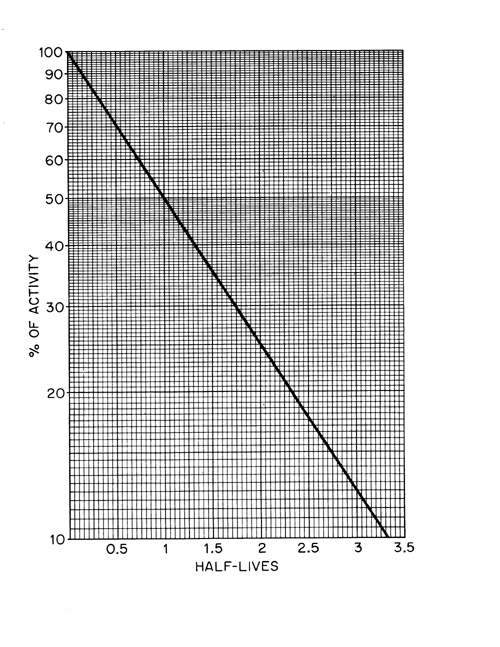
The activity of a pure radioactive substance as a function of time can be obtained from the exponential equation or from decay tables, or by graphical means based on the half-life (see Normalized Decay Chart, Figure 1).
The activity of a radioactive material is expressed as the number of nuclear transformations per unit time. The fundamental unit of radioactivity, the curie (Ci), is defined as 3.700 × 1010 nuclear transformations per second. The millicurie (mCi) and microcurie (µCi) are commonly used subunits. The “number of nuclear transformations per unit time” is the sum of rates of decay from all competing modes of disintegration of the parent nuclide. Before the activity of any given radionuclide in a measured specimen can be expressed in curies, it is often necessary to know the abundance(s) of the emitted radiation(s) measured.
Geometry
The validity of relative calibration and measurement of radionuclides is dependent upon the reproducibility of the relationship of the source to the detector and its surroundings. Appropriate allowance must be made for source configuration.
Background
Cosmic rays, radioactivity present in the detector and shielding materials, and radiation from nearby radioactive sources not properly shielded from the measuring equipment, all contribute to the background count rate. All radioactivity measurements must be corrected by subtracting the background count rate from the gross count rate in the test specimen.
Statistics of Counting
Since the process of radioactive decay is a random phenomenon, the events being counted form a random sequence in time. Therefore, counting for any finite time can yield only an estimate of the true counting rate. The precision of this estimate, being subject to statistical fluctuations, is dependent upon the number of counts accumulated in a given measurement and can be expressed in terms of the standard deviation 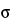 . An estimate for
. An estimate for 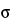 is
is
where n is the number of counts accumulated in a given measurement. The probability of a single measurement falling within
of the mean of a great many measurements is 0.68. That is, if many measurements of n counts each were to be made, approximately two-thirds of the observations would lie within
of the mean, and the remainder outside.
Because of the statistical nature of radioactive decay, repeated counting of an undisturbed source in a counting assembly will yield count-rate values in accordance with the frequency of a normal distribution. Deviations in these values from the normal distribution conform to the 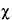 2 test. For this reason, the
2 test. For this reason, the 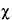 2 test is frequently applied to determine the performance and correct operation of a counting assembly. In the selection of instruments and conditions for assay of radioactive sources, the figure of merit
2 test is frequently applied to determine the performance and correct operation of a counting assembly. In the selection of instruments and conditions for assay of radioactive sources, the figure of merit 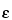 2/B should be maximized (where
2/B should be maximized (where 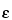 = counter efficiency = observed count rate/sample disintegration rate, and B = background count rate).
= counter efficiency = observed count rate/sample disintegration rate, and B = background count rate).
Counting Losses
The minimum time interval that is required for the counter to resolve two consecutive signal pulses is known as the dead time. The dead time varies typically from the order of microseconds for proportional and scintillation counters, to hundreds of microseconds for Geiger-Müller counters. Nuclear events occurring within the dead time of the counter will not be registered. To obtain the corrected count rate, R, from the observed count rate, r, it is necessary to use the formula:
in which 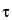 is the dead time. The foregoing correction formula assumes a nonextendable dead time. Thus, for general validity, the value of r
is the dead time. The foregoing correction formula assumes a nonextendable dead time. Thus, for general validity, the value of r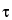 should not exceed 0.1. The observed count rate, r, refers to the gross specimen count rate and is not to be corrected for background before use in the foregoing equation.
should not exceed 0.1. The observed count rate, r, refers to the gross specimen count rate and is not to be corrected for background before use in the foregoing equation.
Calibration Standards
Perform all radioactivity assays using measurement systems calibrated with appropriately certified radioactivity standards. Such calibration standards may be purchased either direct from the National Institute of Standards and Technology or from other sources that have established traceability to the National Institute of Standards and Technology through participation in a program of inter-comparative measurements. Where such calibration standards are unavailable, the Pharmacopeia provides the nuclear decay data required for calibration. These data, as well as half-life values, are obtained from the Evaluated Nuclear Structure Data File of the Oak Ridge Nuclear Data Project, and reflect the most recent values at the time of publication.
Carrier
The total mass of radioactive atoms or molecules in any given radioactive source is directly proportional to the activity of the radionuclide for a given half-life, and the amount present in radiopharmaceuticals is usually too small to be measured by ordinary chemical or physical methods. For example, the mass of 131I having an activity of 100 mCi is 8 × 10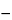 7 g. Since such small amounts of material behave chemically in an anomalous manner, carriers in the form of nonradioactive isotopes of the same radionuclide may be added during processing to permit ready handling. In many cases, adsorption can be prevented merely by increasing the hydrogen-ion concentration of the solution. Amounts of such material, however, must be sufficiently small that undesirable physiological effects are not produced. The term “carrier-free” refers only to radioactive preparations in which nonradioactive isotopes of the radionuclide are absent. This implies that radioactive pharmaceuticals produced by means of (n,
7 g. Since such small amounts of material behave chemically in an anomalous manner, carriers in the form of nonradioactive isotopes of the same radionuclide may be added during processing to permit ready handling. In many cases, adsorption can be prevented merely by increasing the hydrogen-ion concentration of the solution. Amounts of such material, however, must be sufficiently small that undesirable physiological effects are not produced. The term “carrier-free” refers only to radioactive preparations in which nonradioactive isotopes of the radionuclide are absent. This implies that radioactive pharmaceuticals produced by means of (n, 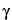 ) reactions cannot be considered carrier-free.
) reactions cannot be considered carrier-free.
The activity per unit volume or weight of a medium or vehicle containing a radionuclide either in the carrier-free state or in the presence of carrier is referred to as the radioactive concentration, whereas the term specific activity is used to express the activity of a radionuclide per gram of its element.
Radiochemical Purity
Radiochemical purity of a radiopharmaceutical preparation refers to the fraction of the stated radionuclide present in the stated chemical form. Radiochemical impurities in radiopharmaceuticals may result from decomposition and from improper preparative procedures. Radiation causes decomposition of water, a main ingredient of most radiopharmaceuticals, leading to the production of reactive hydrogen atoms and hydroxyl radicals, hydrated electrons, hydrogen, hydrogen ions, and hydrogen peroxide. The last-mentioned is formed in the presence of oxygen radicals, originating from the radiolytic decomposition of dissolved oxygen. Many radiopharmaceuticals show improved stability if oxygen is excluded. Radiation may also affect the radiopharmaceutical itself, giving rise to ions, radicals, and excited states. These species may combine with one another and/or with the active species formed from water. Radiation decomposition may be minimized by the use of chemical agents that act as electron or radical scavengers. Electrons trapped in solids cause discoloration due to formation of F-centers and the darkening of glass containers for radiopharmaceuticals, a situation that typifies the case. The radiochemical purity of radiopharmaceuticals is determined by column, paper, and thin-layer chromatography or other suitable analytical separation techniques as specified in the individual monograph.
Radionuclidic Purity
Radionuclidic purity of a radiopharmaceutical preparation refers to the proportion of radioactivity due to the desired radionuclide in the total radioactivity measured. Radionuclidic purity is important in the estimation of the radiation dose received by the patient when the preparation is administered. Radionuclidic impurities may arise from impurities in the target materials, differences in the values of various competing production cross-sections, and excitation functions at the energy or energies of the bombarding particles during production.
Terms and Definitions
The date of manufacture is the date on which the manufacturing cycle for the finished product is completed.
The date of assay is the date (and time, if appropriate) when the actual assay for radioactivity is performed.
The date of calibration is an arbitrary assigned date and time to which the radioactivity of the product is calculated for the convenience of the user.
The expiration date is the date that establishes a limit for the use of the product. The expiration period (i.e., the period of time between the date of manufacture and the expiration date) is based on a knowledge of the radioactive properties of the product and the results of stability studies on the finished dosage form.
Labeling
Individual radiopharmaceutical monographs indicate the expiration date, the calibration date, and the statement, “Caution—Radioactive Material.” The labeling indicates that in making dosage calculations, correction is to be made for radioactive decay, and also indicates the radioactive half-life of the radionuclide. Articles that are Injections comply with the requirements for Labeling under Injections  1
1 , and those that are Biologics comply with the requirements for Labeling under Biologics
, and those that are Biologics comply with the requirements for Labeling under Biologics  1041
1041 .
.
IDENTIFICATION AND ASSAY OF RADIONUCLIDES
Instrumentation
ionization chambers
An ionization chamber is an instrument in which an electric field is applied across a volume of gas for the purpose of collecting ions produced by a radiation field. The positive ions and negative electrons drift along the lines of force of the electric field, and are collected on electrodes, producing an ionization current. In a properly designed well-type ionization chamber, the ionization current should not be too dependent on the position of the radioactive specimen, and the value of the current per unit activity, known as the calibration factor, is characteristic of each gamma-ray-emitting radionuclide.
The ionization current produced in an ionization chamber is related to the mean energy of the emitted radiation and is proportional to the intensity of the radiation. If standard sources of known disintegration rates are used for efficiency calibration, the ionization chamber may then be used for activity determinations between several microcuries and several hundred millicuries or more. The upper limit of activity that may be measured in an ionization chamber usually is not sharply defined and may be limited by saturation considerations, range of the amplifier, and design of the chamber itself. The data supplied with or obtained from a particular instrument should be reviewed to ascertain the useful ranges of energies and intensities of the device.
Reproducibility within approximately 5% or less can be readily obtained in about 10 seconds, with a deep re-entrant well-type chamber. The most commonly used form of ionization chamber for measurement of the activities of radiopharmaceuticals is known as a dose calibrator.
Although the calibration factor for a radionuclide may be interpolated from an ionization chamber energy-response curve, there are a number of sources of error possible in such a procedure. It is therefore recommended that all ionization chamber calibrations be performed with the use of authentic reference sources of the individual radionuclides, as described hereinafter.
The calibration of a dose calibrator should be maintained by relating the measured response of a standard to that of a long-lived performance standard, such as radium 226 in equilibrium with its daughters. The instrument must be checked daily with the 226Ra or other source to ascertain the stability over a long period of time. This check should include performance standard readings at all radionuclide settings employed. To obtain the activity (Ax) of the radionuclide being measured, use the relationship:
in which Rn is the new reading for the radium or other source, Rc is the reading for the same source obtained during the initial calibration procedure, and R is the observed reading for the radionuclide specimen. Obviously, any necessary corrections for radioactive decay of the reference source must first be applied. Use of this procedure should minimize any effects due to drift in the response of the instrument. The recommended activity of the 226Ra or other monitor used in the procedure described above is 75 to 150 µCi. It is recommended also that the reproducibility and/or stability of multirange instruments be checked for all ranges with the use of appropriate standards.
The size and shape of a radioactive source may affect the response of a dose calibrator, and it is often necessary to apply a small correction when measuring a bulky specimen.
scintillation and semiconductor detectors
When all or part of the energy of beta or gamma radiation is dissipated within scintillators, photons of intensity proportional to the amount of dissipated energy are produced. These pulses are detected by an electron multiplier phototube and converted to electrical pulses, which are subsequently analyzed with a pulse-height analyzer to yield a pulse-height spectrum related to the energy spectrum of the radiation emitted by the source. In general, a beta-particle scintillation pulse-height spectrum approximates the true beta-energy spectrum, provided that the beta-particle source is prepared in such a manner that self-absorption is minimized. Beta-ray spectra may be obtained by using calcium fluoride or anthracene as the scintillator, whereas gamma-ray spectra are usually obtained with a thallium-activated sodium iodide crystal or a large-volume lithium-drifted germanium semiconductor detector. The spectra of charged particles also may be obtained using silicon semiconductor detectors and/or gas proportional counters. Semiconductor detectors are in essence solid-state ionization chambers, but the energy required to create an electron-hole pair or to promote an electron from the valence band to the conduction band in the semiconductor is about one-tenth the energy required for creation of an ion-pair in a gas-filled ionization chamber or proportional counter and is far less than the energy needed to produce a photon in a NaI(Tl) scintillation crystal. In gamma-ray spectrometry, a Ge(Li) detector can yield an energy resolution of 0.33% for 1.33 MeV gamma-rays from 60Co, while a 3- × 3-inch NaI(Tl) crystal can give a value of 5.9% for the same gamma-ray energy. The energy resolution is a measure of the ability to distinguish the presence of two gamma rays closely spaced in energy and is defined by convention as the full width of the photopeak at its half maximum (FWHM), expressed in percentage of the photopeak energy.
Gamma-ray spectra exhibit one or more sharp, characteristic photopeaks, or full-energy peaks, as a result of total absorption in the detector of the full energy of gamma radiations from the source; these photopeaks are useful for identification purposes. Other secondary peaks are observed as a consequence of backscatter, annihilation radiation, coincidence summing, fluorescent X-rays, etc., accompanied by a broad band known as the Compton continuum arising from scattering of the photons in the detector and from surrounding materials. Since the photopeak response varies with gamma-ray energy, calibration of a gamma-ray spectrometer should be achieved with radionuclide standards having well-known gamma-ray energies and emission rates. The shape of the gamma-ray spectrum is dependent upon the shape and size of the detector and the types of shielding materials used.
When confirming the identity of a radionuclide by gamma-ray spectrometry, it is necessary to make a comparison of the specimen spectrum with that of a specimen of known purity of the same radionuclide obtained under identical instrument parameters and specimen geometry. Where the radionuclides emit coincident X- or gamma-radiations, the character of the pulse-height distribution often changes quite dramatically because of the summing effect of these coincident radiations in the detector as the efficiency of detection is increased (e.g., by bringing the source closer to the detector). Such an effect is particularly evident in the case of iodine 125. Among the more useful applications of gamma-ray spectrometry are those for the identification of radionuclides and the determination of radionuclidic impurities.
Where confirmation of the identity of a given radionuclide by means of a direct comparison with the spectrum of a specimen of the same radionuclide of known purity is not possible, the identity of the radionuclide in question must then be established by the following method. Two or more of the following nuclear decay scheme parameters of the radionuclide specimen to be identified shall be measured, and agreement shall be within ±10%: (1) half-life, (2) energy of each gamma- or X-ray emitted, (3) the abundance of each emission, and (4) Emax for those radionuclides that decay with beta-particle emissions. Such measurements are to be performed as directed in the Identification and Assay sections of this chapter. Agreement of two or more of the measured parameters with the corresponding published nuclear decay scheme data constitutes confirmation of the identity of the radionuclide.
liquid-scintillation counters
Alpha- and beta-emitting radionuclides may be assayed with the use of a liquid-scintillation detector system. In the liquid scintillator, the radiation energy is ultimately converted into light quanta that are usually detected by two multiplier phototubes so arranged as to count only coincidence radiation. The liquid scintillator is a solution consisting of a solvent, primary and secondary solutes, and additives. The charged particle dissipates its energy in the solvent, and a fraction of this energy is converted into fluorescence in the primary solute. The function of the secondary solute is to shift the fluorescence radiation to longer wavelengths that are more efficiently detected by the multiplier phototubes. Frequently used solvents are toluene and p-xylene; primary solutes are 2,5-diphenyloxazole (PPO) and 2-(4¢-tert-butylphenyl)-5-(4-biphenylyl)-1,3,4-oxadiazole (butyl-PBD); and secondary solutes are 2,2¢-p-phenylenebis[4-methyl-5-phenyloxazole] (dimethyl-POPOP) and p-bis(o-methylstrylyl)benzene (bis-MSB). As a means of attaining compatibility and miscibility with aqueous specimens to be assayed, many additives, such as surfactants and solubilizing agents, are also incorporated into the scintillator. For an accurate determination of radioactivity of the specimen, care must be exercised to prepare a specimen that is truly homogeneous. The presence of impurities or color in solution causes a decrease in photon output of the scintillator; such a decrease is known as quenching. Accurate radioactivity measurement requires correcting for count-rate loss due to quenching.
The disintegration rate of a beta-particle source may be determined by a procedure in which the integral count rate of the specimen is measured as a function of the pulse-height discriminator bias, and the emission rate is then obtained by extrapolation to zero bias. Energetic alpha-particle emitters may be similarly measured by this method.
Identification
A radionuclide can be identified by its mode of decay, its half-life, and the energies of its nuclear emissions.
The radioactive half-life is readily determined by successive counting of a given source of the radionuclide over a period of time that is long compared to its half-life. The response of the counting assembly when employed for the decay measurement of long-lived radionuclides should be monitored with an even longer-lived reference source to assess and compensate for errors arising from electronic drift. In the case of short-lived radionuclides, when the counting period constitutes a significant fraction of the half-life of the radionuclide, the recorded count rate must be corrected to the time when the count is initiated, as follows:
in which Rt is the count rate at the beginning of a counting period, r is the count rate observed over the entire counting period, t is the duration of the counting period, 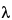 is the decay constant of the radionuclide, and e is the base of the natural logarithm. When t is small compared to the half-life of the radionuclide under study so that
is the decay constant of the radionuclide, and e is the base of the natural logarithm. When t is small compared to the half-life of the radionuclide under study so that 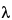 t < 0.05, then (1 – e–
t < 0.05, then (1 – e–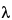 t) approaches
t) approaches 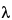 t, and no such correction is necessary.
t, and no such correction is necessary.
The energy of nuclear emissions is often determined by the maximum range of penetration of the radiation in matter (in the case of alpha- and beta-particles) and by the full-energy peak or photopeak in the gamma-ray spectrum (in the case of X- and gamma-rays). Since beta-particles are emitted with a continuous energy spectrum, the maximum beta-energy, Emax, is a unique index for each beta-emitting radionuclide. In addition to the maximum range and energy spectrum of the beta-particles, the absorption coefficient, when obtained under reproducible counting conditions, can serve as a reliable index for identification of a beta-emitter. Fortuitously, beta-particles are absorbed in matter in an approximately exponential manner, and a plot of the logarithm of the beta-particle count rate as a function of the absorber thickness is known as the absorption curve. The initial portion of the absorption curve shows linearity from which the absorption coefficient can be obtained. The maximum range is determined by the use of absorbers of varying thickness, and the energy spectrum is measured by beta-ray scintillation spectrometry.
The absorption of gamma-rays in matter is strictly exponential, but the half-value layers of attenuation have not been very useful for the purpose of radionuclide characterization. Gamma-rays from each isomeric transition are mono-energetic; their energy can be directly measured by gamma-ray spectrometry. Because of their high energy resolution, solid-state detectors [Ge(Li)] are vastly superior to scintillation detectors [NaI(Tl)] in gamma-ray spectrometry.
The activities of radiopharmaceutical solutions are frequently in the range of millicuries per mL. Such solutions usually must be extensively diluted before they can be accurately assayed. The diluent should be compatible with the radiopharmaceutical with respect to factors such as pH and redox potentials, so that no hydrolysis or change in oxidation state occurs upon dilution, which could lead to adsorption and separation of the radionuclide from solution.
beta-emitting radionuclides
Mass Absorption Coefficient Procedure—
Deposit and dry an aliquot of the radioactive phosphorus 32 solution on a thin plastic film to minimize backscattering, and place it under a suitable counter. Determine the counting rates successively, using not less than six different “thicknesses” of aluminum each between 20 and 50 mg/cm2 and a single absorber thicker than 800 mg/cm2, which is used to measure the background. (The absorbers are inserted between the test specimen and the counter but are placed nearer the counter window to minimize scattering.) Net beta-particle count rates are obtained after subtraction of the count rate found with the absorber having a thickness of 800 mg/cm2 or greater. Plot the logarithm of the net beta-particle count rate as a function of the total absorber “thickness.” The total absorber “thickness” is the “thickness” of the aluminum absorbers plus the “thickness” of the counter window (as stated by the manufacturer) plus the air-equivalent “thickness” (the distance in centimeters of the specimen from the counter window multiplied by 1.205 mg/cm3 at 20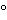 and 76 cm of mercury), all expressed in mg/cm2. An approximately straight line results.
and 76 cm of mercury), all expressed in mg/cm2. An approximately straight line results.
Choose two total absorber “thicknesses” that differ by 20 mg/cm2 or more and that fall on the linear plot, and calculate the mass absorption coefficient, µ, by the equation:
in which t1 and t2 represent the total absorber “thicknesses,” in mg/cm2, t2 being the thicker absorber, and Nt1 and Nt2 being the net beta-particle rates with the t1 and t2 absorbers, respectively.
For characterization of the radionuclide, the mass absorption coefficient should be within ±5% of the value found for a pure specimen of the same radionuclide when determined under identical counting conditions and geometry.
Other Methods of Identification—
Other methods for determining the identity of a beta emitter also rely upon the determination of Emax. This may be accomplished in several ways. For example, (1) utilization of the range energy relationships of beta particles in an absorber, or (2) determination of Emax from a beta-particle spectrum obtained on an energy-calibrated beta-spectrometer using a thin source of the radionuclide (see Scintillation and Semiconductor Detectors in this chapter).
gamma-emitting radionuclides
The gamma-ray spectrum of a radionuclide is a valuable tool for the qualitative identification of gamma-ray emitting radionuclides. The full-energy peak, or the photopeak, is identified with the gamma-ray transition energy that is given in the decay scheme of the radionuclide.
In determining radionuclidic identity and purity, the gamma-ray spectrum of a radioactive substance is obtained with either a NaI(Tl) crystal or a semiconductor Ge(Li) detector. The latter has an energy resolution more than an order of magnitude better than the former and is highly preferred for analytical purposes. The spectrum obtained shall be identical in shape to that of a specimen of the pure radionuclide, measured with the same detection system and in the same geometry. The gamma-ray spectrum of the radiopharmaceutical shall contain only photopeaks identifiable with the gamma-ray transition energies found in the decay scheme of the same radionuclide. For low geometrical efficiencies, the areas under the photopeaks, after correction for the measured detector efficiency, shall be proportional to the abundances or emission rates of the respective gamma-rays in the radionuclide.
radionuclidic impurities
Because they are extremely toxic, alpha-emitting nuclides must be strictly limited in radiopharmaceutical preparations. Procedures for identifying beta- and gamma-active radionuclides as given in the foregoing text are applicable to the detection of gamma and usually beta contaminants.
The gross alpha-particle activity in radiopharmaceutical preparations can be measured by the use of a windowless proportional counter or a scintillation detector employing a silver-activated zinc-sulfide phosphor or by the techniques of liquid-scintillation counting.
The heavy ionization caused by alpha particles allows the measurement of alpha-emitting radionuclides in the presence of large quantities of beta- and gamma-active nuclides by the use of appropriate techniques for discriminating the amplitudes of signal pulses. In proportional counting, the operating voltage region for counting alpha particles, referred to as the “alpha plateau,” is considerably lower than the “beta plateau” for counting beta and gamma radiations. Typical “alpha plateau” and “beta plateau” voltage settings with P-10 counting gas are 900 to 1300 and 1600 to 2000 volts, respectively.
When silver-activated zinc-sulfide phosphor is employed for alpha-particle detection, the alpha particles can be distinguished from other interfering radiation by pulse-height discrimination. Care must be exercised to minimize self-absorption at the source whenever specimens are prepared for alpha-particle counting.
Assay
beta-emitting radionuclides
Procedure—
The disintegration rate (A) of a beta-particle-emitting specimen is obtained by counting a quantitatively deposited aliquot in a fixed geometry according to the formula:
in which 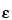 is the counting efficiency of the counter; fr is the correction factor for counter dead time; fb is the correction factor for backscatter; and fs is the correction factor for self-absorption. The count rate for zero absorber is obtained by extrapolation of the initial linear portion of the absorption curve to zero absorber “thickness,” taking into consideration the mg/cm2 “thickness” of specimen coverings, counter window, and the intervening air space between specimen and the counter window. The counter efficiency,
is the counting efficiency of the counter; fr is the correction factor for counter dead time; fb is the correction factor for backscatter; and fs is the correction factor for self-absorption. The count rate for zero absorber is obtained by extrapolation of the initial linear portion of the absorption curve to zero absorber “thickness,” taking into consideration the mg/cm2 “thickness” of specimen coverings, counter window, and the intervening air space between specimen and the counter window. The counter efficiency, 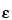 , is determined by use of a long-lived secondary standard with similar spectral characteristics. RaD + E has frequently been used for efficiency calibration of counters for phosphorus 32. By the use of identical measurement conditions for the specimen and the standard (and extrapolation to zero absorber), the ratio of the values of fr, fb, and fs for the standard and the specimen approaches unity.
, is determined by use of a long-lived secondary standard with similar spectral characteristics. RaD + E has frequently been used for efficiency calibration of counters for phosphorus 32. By the use of identical measurement conditions for the specimen and the standard (and extrapolation to zero absorber), the ratio of the values of fr, fb, and fs for the standard and the specimen approaches unity.
The previous relationship is valid also when the counter has been calibrated with a standard of the radionuclide to be assayed. In this case, however, the extrapolations to zero absorber “thickness” for the specimen and standard are not required, as the two absorption corrections cancel for a given geometry.
Another useful and frequently employed method for the determination of the disintegration rate of beta-emitting radionuclides is liquid-scintillation counting, which also utilizes an extrapolation of the specimen count rate to zero pulse-height discriminator bias.
gamma-emitting radionuclides
For the assay of gamma-emitting radionuclides, three methods are provided. The selection of the preferred method is dictated by the availability of a calibration standard of the radionuclide to be assayed and the radionuclidic purity of the article itself.
Direct comparison with a calibration standard is required if a calibration standard of the radionuclide to be assayed is available and if the upper limit of conceivable error in the activity determination arising from the presence of radionuclidic impurities has been determined to be less than 3%. If the required calibration standard is not routinely available, as would probably be the case for a short-lived radionuclide, but was available at some time prior to the performance of the assay for determination of efficiency of the counting system for the radionuclide to be assayed, use a calibrated counting system, provided the radionuclidic impurity content of the specimen meets the requirements stated for the direct comparison method. If the requirements for either of the first two methods cannot be met, use the method for determination of activity from a calibration curve.
With the exception of the first method, the counting systems used are monitored for stability. This requirement is met by daily checks with a long-lived performance check source and weekly checks with at least three sources covering a broad range of gamma-ray emission energies (e.g., 57Co, 137Cs, and 60Co). If a discrepancy for any of the aforementioned measurements is found, either completely recalibrate or repair and recalibrate the system prior to further use.
Assay by Direct Comparison with a Calibration Standard—
An energy selective measurement system (e.g., pulse-height analyzer) is not required for this procedure. Use either an ionization chamber or an integral counting system with a NaI(Tl) detector. A consistently reproducible geometrical factor from specimen to specimen is essential for accurate results. With proper precautions, the accuracy of this method approaches the accuracy with which the disintegration rate of the calibration standard is known.
Determine the counting rate of the detector system for a calibration standard of the radionuclide to be assayed (e.g., active enough to give good measurement statistics in a reasonable time, but not so active as to cause serious dead-time problems), selecting such a standard as to provide optimum accuracy with the particular assembly used. Place an accurately measured aliquot of the unknown assay specimen (diluted, if necessary) in a container identical to that used for the standard, and measure this specimen at approximately the same time and under the same geometrical conditions as for the standard. If the elapsed time between the measurements of the calibration standard and the specimen exceeds 12 hours, check the stability of the measurement system within 8 hours of the specimen measurement time with a long-lived performance check source. Record the system response with respect to the same check source at the time of calibration, and if subsequent checks exceed the original recorded response by more than ±3%, recalibration is required. Correct both activity determinations for background, and calculate the activity, in µCi per mL, by the formula:
in which S is the µCi strength of the standard, D is the dilution factor, and g and b are the measured values of counting rate for the specimen and the standard, respectively.
Assay with a Calibrated Integral Counting System—
The procedure and precautions given for the preceding direct-comparison method apply, except that the efficiency of the detector system is determined and recorded for each radionuclide to be assayed, rather than simply recording the counting rate of the standard. Thus, the efficiency for a given radionuclide, x, is determined by 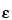 x = bx/sx, in which bx is the counting rate, corrected for background and dead-time, for the calibration standard of the radionuclide, x, and sx is the corresponding activity of the certified calibration standard in nuclear transformations per second. For subsequent specimen assays, the activity is given by the formula:
in which D is the dilution factor, gx is the specimen counting rate (corrected for background and dead-time), and
x = bx/sx, in which bx is the counting rate, corrected for background and dead-time, for the calibration standard of the radionuclide, x, and sx is the corresponding activity of the certified calibration standard in nuclear transformations per second. For subsequent specimen assays, the activity is given by the formula:
in which D is the dilution factor, gx is the specimen counting rate (corrected for background and dead-time), and 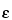 x is the corresponding efficiency for the radionuclide.
x is the corresponding efficiency for the radionuclide.
Determination of Activity from a Calibration Curve—
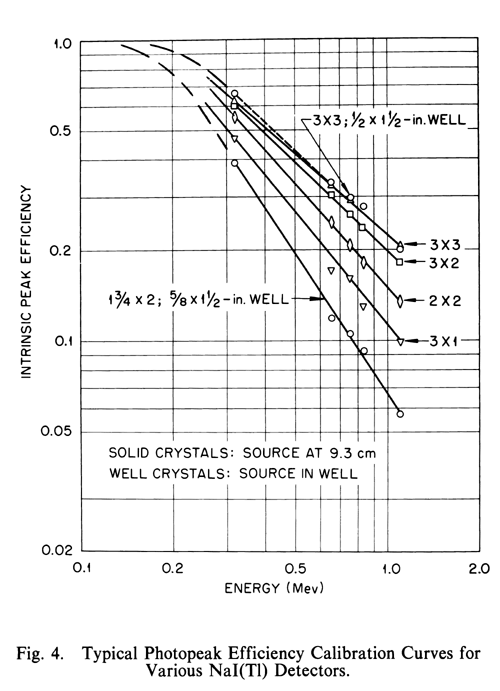
Versatility in absolute gamma-ray intensity measurements can be achieved by employing multi-channel pulse-height analysis. The photopeak efficiency of a detector system can be determined as a function of gamma-ray energy by means of a series of gamma-ray emission rate standard specimens, and the gamma-ray emission rate of any radionuclide for which no standard is available can be determined by interpolation from this efficiency curve. However, exercise care to ensure that the efficiency curve for the detector system is adequately defined over the entire region of interest by using a sufficient number of calibration points along the photopeak-energy axis.
Selection of a Counting Assembly—
A gamma-ray spectrometer is used for the identification of radionuclides that emit X-rays or gamma rays in their decay. Requirements for an assembly suitable for identification and assay of the radionuclides used in radiopharmaceuticals are that (a) the resolution of the detector based on the 662-keV photopeak of 137Cs-137mBa must be 8.0% or better, (b) the detector must be equipped with a specimen holder designed to facilitate exact duplication of counting geometry, and (c) the pulse-height analyzer must have enough channels to delineate clearly the photopeak being observed.
Procedure—
Minimal requirements for the maintenance of instrument calibrations shall consist of weekly performance checks with a suitable reference source and a complete recalibration semi-annually. Should the weekly performance check deviate from the value determined at the time of calibration by more than 4.0%, a complete recalibration of the instrument is required at that time.
This method involves three basic steps, namely photopeak integration, determination of the photopeak efficiency curve, and calculation of the activity of the specimen.
photopeak integration—
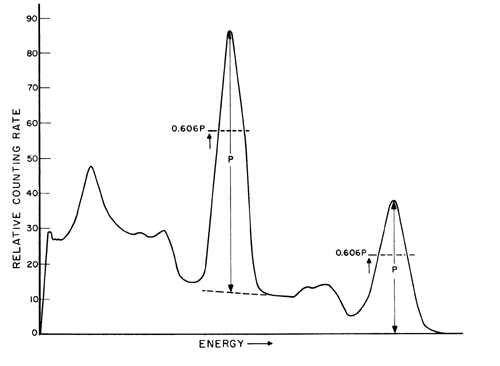
The method for the determination of the required photopeak area utilizes a Gaussian approximation for fitting the photopeak. A fixed fraction of the total number of photopeak counts can be obtained by taking the peak width, a, at some fraction of the maximum, where the shape has been experimentally found to be very close to Gaussian, and multiplying by the counting rate of the peak channel, P, after correction for any Compton and background contributions to the peak channel count rate. This background usually can be adequately determined by linear interpolation. This is illustrated in Figure 2.
Fig. 2 Typical Gamma-ray Spectrum Showing the Selection of the Peak Channel Counting Rate, P, after the Correction for Compton and Background Contributions.
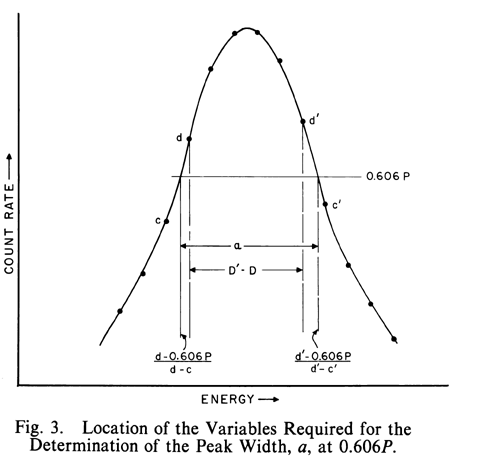
The photopeak-curve shape is closest to a straight line at 0.606P, and the contribution of the fractional channels to a can be accurately estimated by interpolation. Calculate a by the equation:
in which c and d and also c¢ and d¢ are the single channel counting rates on either side of 0.606P, and D and D¢ are the channel numbers (locations) of d and d¢, respectively. The location of the required variables on the photopeak is illustrated in Figure 3.
From the known values for the counting rate in the peak channel of the photopeak, P, and the width of the peak at 0.606P, a, a calibrated fraction of the photopeak area is then obtained from the product, (aP).
To summarize the procedures involved in obtaining a calibrated fraction of a photopeak area using this method, the necessary steps or calculations are presented below in a stepwise manner:
(1) Subtract any Compton and background contributions from the photopeak to be measured.
(2) Determine the counting rate of the peak channel (maximum channel counting rate after subtracting Compton and background), P.
(3) Multiply P by 0.606, and locate the horizontal line corresponding to the peak width, a.
(4) Obtain the peak width, a, by inserting the values of variables (obtained as shown in the preceding figure) into the equation defining a.
(5) The desired calibrated fraction of the peak area is then equal to the product of a times P or F = aP, where F is a fractional area of the peak proportional to the emission rate of the source.
This method provides a quick and accurate means of determining the gamma-ray emission rate of sources while avoiding, to a large extent, subjective estimates of the detailed shape of the tails of the peaks. The error due to using the maximum channel counting rate, rather than the theoretical maximum or peak channel rate, is of the order of 1.0% if a is 6 or greater.
photopeak efficiency calibration—
Radionuclides such as those listed in the accompanying table together with some of their nuclear decay data are available as certified reference standards.* A sufficient number of radioactive standard reference sources should be selected in order to obtain the calibration curve over the desired range. Where possible, standard sources of those radionuclides that are to be assayed should be included.
| Principal Photon Emissions | Energy (ke V) |
Photons per 100 Disintegrations |
| 133Ba (T1/2 = 10.5 years) | ||
| K |
30.97 | 63.4 |
| K |
30.62 | 34.2 |
| K |
35.0 | 22.8 |
| 53.15 | 2.14 | |
| 79.62 | 2.55 | |
| 80.99 | 33.0 | |
| 276.39 | 6.9 | |
| 302.83 | 17.8 | |
| 356.0 | 60.0 | |
| 383.85 | 8.7 | |
| 137Cs |
||
| K |
32.19 | 3.82 |
| K |
31.82 | 2.07 |
| K |
36.4 | 1.39 |
| Weighted Mean(4) | (32.9) | (7.28) |
| 661.6 | 89.98 | |
| 22Na (T1/2 = 2.60 years) | ||
| h |
511 | 179.80(5) |
| 1274.54 | 99.94 | |
| 60Co(T1/2 = 5.27 years) | ||
| 1173.2(6) | 100.0 | |
| 1332.5(6) | 100.0 | |
| 57Co(T1/2 = 270.9 days) | ||
| SXK | 7.0 | 56.0 |
| 14.4 | 9.5 | |
| 122.06 | 85.51 | |
| 136.47 | 10.60 | |
| Weighted Mean | (125.0) | (96.11) |
| ( |
||
| 54Mn (T1/2 = 312.7 days) | ||
| SXK | 6.0 | 25.0 |
| 834.83 | 99.98 | |
| 109Cd |
||
| K |
22.16 | 35.3 |
| K |
21.99 | 18.6 |
| K |
24.9 | 11.4 |
| Weighted Mean(4) | 63.5 | |
| 88.0 | 3.72 | |
| 129I(T1/2 = 1.57 × 107 years) | ||
| K |
29.78 | 37.0 |
| K |
29.46 | 20.0 |
| K |
13.2 | 37.0 |
| 39.58 | 7.52 | |
| Weighted Mean(4) | (31.3) | (77.80) |
|
(1)
In measurements for gamma- (or X-)ray assay purposes, fluorescent radiation from lead shielding (specifically, lead K X-rays
|
||
|
(2)
Only those photon emissions having an abundance
|
||
|
(3)
The K notation refers to X-ray emissions.
|
||
|
(4)
The weighted mean energies and total intensities are given for groups of photons that would not be resolved by a NaI(Tl) detector.
|
||
|
(5)
For this photon intensity to be usable, all emitted positrons must be annihilated in the source material.
|
||
|
(6)
Cascade.
|
||
Calculate the gamma-ray emission rate from the equation:
G = Asb
in which As is the activity, in disintegrations per second, of the standard used, and b is the number of gamma rays per disintegration at that energy. Accurately measure quantities of standard solutions of each radionuclide into identical containers, and determine the fractional photopeak area (F) for each of the standards.
Using the equation 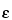 p = F/G, calculate the photopeak efficiency,
p = F/G, calculate the photopeak efficiency, 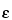 p, and construct a log-log plot of
p, and construct a log-log plot of 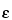 p versus the gamma-ray energy as shown in Figure 4.
p versus the gamma-ray energy as shown in Figure 4.
determination of specimen activity—
In the same manner as in the preparation of the calibration curve, determine the fractional area (F) of the principal photopeak of the specimen under assay or an accurately measured aliquot adjusted to the same volume in an identical container as used for the standards. From the calibration curve, find the value of 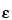 p for this radionuclide. Using the equation G = F/
p for this radionuclide. Using the equation G = F/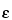 p, calculate the gamma-ray emission rate (G). Calculate the activity (A), in disintegrations per second, of the specimen using the equation A = (G/b)(D), in which b is the number of gamma rays per disintegration and D is the dilution factor. To obtain the activity, in µCi or mCi, divide A by 3.7 × 104 or 3.7 × 107, respectively. The above relationship is equally valid for obtaining the activity of an undiluted specimen or capsule; in this case, the dilution factor, D, is unity.
p, calculate the gamma-ray emission rate (G). Calculate the activity (A), in disintegrations per second, of the specimen using the equation A = (G/b)(D), in which b is the number of gamma rays per disintegration and D is the dilution factor. To obtain the activity, in µCi or mCi, divide A by 3.7 × 104 or 3.7 × 107, respectively. The above relationship is equally valid for obtaining the activity of an undiluted specimen or capsule; in this case, the dilution factor, D, is unity.
*
These certified reference standards are obtainable from the National Institute of Standards and Technology, Washington, DC 20234.
Auxiliary Information— Please check for your question in the FAQs before contacting USP.
| Topic/Question | Contact | Expert Committee |
| General Chapter | Ian DeVeau, Ph.D.
Director, Veterinary Drugs and Radiopharmaceuticals 1-301-816-8178 |
(RMI05) Radiopharmaceuticals and Medical Imaging Agents 05 |
USP32–NF27 Page 358